Curriculum Learning for Mathematical Reasoning: Why Design Matters More Than You Think
Published:
TL;DR
I fine-tuned two models (PHI-2 and a 135M smolLM2) using curriculum learning, and here’s what stood out:
Curriculum design matters — the complexity-based curriculum consistently outperformed the naive answer-length curriculum.
PHI-2 improved notably: the advanced curriculum boosted answer accuracy by +1.37% and even slightly improved formatting accuracy (+0.59%) at the Normal stage.
Naive (answer-length) curriculum hurt performance, reducing PHI-2 answer accuracy by up to -3.51% and formatting accuracy by -12% depending on stage.
Small models (135M) didn’t benefit — smolLM2 showed no positive gains across any curriculum or stage, implying curriculum learning is more effective for medium-sized models.
Introduction
Curriculum-learning based fine-tuning is an approach that is inspired by traditional human studying fashion: incrementally increase the difficulty of studying materials. For example: first kids learn basic math operations in school, then they study more complex concepts like functions, then more complex operations like derivation and integration. Current project is built on the same principle: split math tasks by difficulty and fine-tune the model in a complexity increasing curriculum. This small study tries to answer the question: Does curriculum-learning improve fine-tuning performance of LLMs?
Dataset
I was interested to know how well can LLMs solve maths tasks, so gsm8k was chosen as a dataset because it’s popular, contains enough samples and good answers. Also, it doens’t contain very complex operations, but rather tests the reasononing ability of models.
Gsm8k has 2 variations: main and socratic with longer reasoning and socratic-style questions. Each of variations contains 7473 train samples and 1319 test samples. For my experiments main version was chosen as the importance of socratic-style questions in reasoning chain is a subject to investigate in the future. For now, I wanted a more simple setup.
Example of train sample from main variant of gsm8k dataset
{
'question': 'Natalia sold clips to 48 of her friends in April, and then she sold half as many clips in May. How many clips did Natalia sell altogether in April and May?',
'answer': 'Natalia sold 48/2 = <<48/2=24>>24 clips in May.\nNatalia sold 48+24 = <<48+24=72>>72 clips altogether in April and May.\n#### 72',
}
Curriculum composition
As will be evident from experimental results in the following sections, composition of the curriculum, i.e. the condition for splitting the dataset samples into categories of difficulty can either improve model’s fine-tuning performance or make model worse than the baseline, so it’s cruscial to develop a strategy for effective dataset split.
1. Naive approach - Answer Length
One of the first ideas that came up was to split the dataset based on the answer length, as it seems intuitive that the logner the qustion the more difficult it is. After creating a histogram of question lenghts in the dataset, it looked like a normal distibution, so I decieded to split dataset lengths into percentiles where the 50% of samples belong to ‘normal’ difficulty and 25% for ‘easy’ and ‘difficult’.
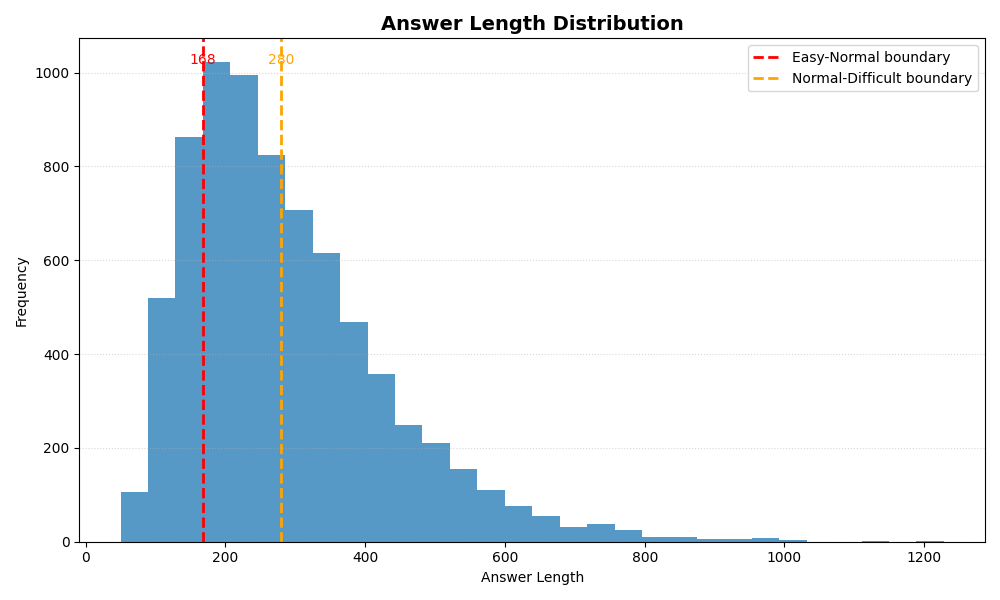
Number of samples in each category:
easy: 1488 samples
normal: 2737 samples
difficult: 3248 samples
2. Composed approach - Complexity Score
For the more advanced option, I decided to use some kind of a composition of several scores. More specifically, to me it seemed reasonable to use length of the answer \(L_a\), difficulty of mathematical operations in question \(OP_q\), and amount of numbers in question \(N_q\). Eventually I came up with this formula for the question difficulty estimation:
\[\displaylines{ Sample\_Complexity\_Score = L_a + (OP_q * N_q) }\]also, difficulty of mathematical operations \(OP_q\) is a weighted composition of amounts of different math operations:
\[\displaylines{ OP_q = additions + subtractions + (multiplications * 1.5) + (divisions * 1.5). }\]After calculating the score of each sample, all samples were equally splitted into 3 categories (‘easy’,’normal’,’difficult’) with 2491 sampels in each category.
Samples difficulties range from 3 to 137, where lower score represents easier task. Distribution of samples difficulties is presented in the follwoing figure:
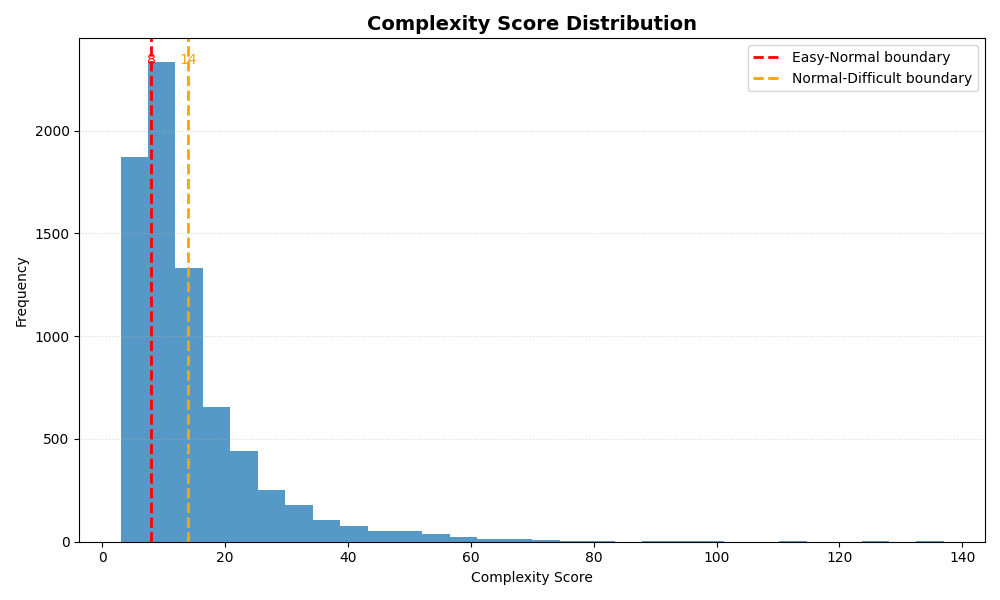
Number of samples in each category:
easy: 2491 samples
normal: 2491 samples
difficult: 2491 samples
Sample from ‘easy’ category:
{
'question': 'A carpenter made ten tables for this month. Last month, he made three fewer tables than this month. How many tables did the carpenter make in total?',
'answer': 'The carpenter made 10 - 3 = <<10-3=7>>7 tables last month.\nSo, the carpenter made 10 + 7 = <<10+7=17>>17 tables in all.\n#### 17'
}
copmlexity_score = 3.0
Sample from ‘normal’ category:
{
'question': 'Michael bought 6 crates of egg on Tuesday. He gave out 2 crates to Susan, who he admires and bought another 5 crates on Thursday. If one crate holds 30 eggs, how many eggs does he have now?',
'answer': 'He had 6 crates and then gave out 2 so he now has 6-2 = <<6-2=4>>4 crates left\nHe bought an additional 5 crates for a total of 4+5 = <<4+5=9>>9 crates\nEach crate has 30 eggs so he has 30*9 = <<30*9=270>>270 eggs\n#### 270'
}
copmlexity_score = 8
Sample from ‘difficult’ category:
{
'question': 'Mr. Ha owns 5 more silver dollars than Mr. Phung. Mr. Phung has 16 more silver dollars than Mr. Chiu has. If Mr. Chiu has 56 silver dollars, how many silver dollars the three have in total?',
'answer': 'Mr. Chiu has 56 silver dollars.\nIf Mr. Phung has 16 more silver dollars than Mr. Chiu, then his total silver dollars is 56+16 = <<16+56=72>>72\nThe total number of silver dollars that Mr. Ha owns is 72 +5= <<72+5=77>>77\nCombined, together they have 77+72+56 = <<77+72+56=205>>205 silver dollars\n#### 205'
}
copmlexity_score = 14.0
Experiments
Fine-tuning
Models were fine-tuned with Huggingface SFTTrainer with the following settings:
training_args = SFTConfig(
completion_only_loss=False,
dataloader_persistent_workers=True,
dataloader_num_workers=16,
gradient_accumulation_steps=4,
learning_rate=3e-4,
logging_steps=10,
logging_first_step=True,
load_best_model_at_end=False,
num_train_epochs=2,
per_device_train_batch_size=32,
packing=False,
report_to="wandb",
save_strategy="epoch",
fp16=True,
warmup_steps=2,
)
Also I used the following configuration of LoRA using PEFT:
lora_config = LoraConfig(
r=16,
lora_alpha=32,
lora_dropout=0.1,
bias="none",
task_type="CAUSAL_LM",
)
target_modules are architecture-dependant:
- PHI2:
target_modules=["Wqkv", "fc1", "fc2"] - smolLm2:
target_modules=["q_proj", "k_proj", "v_proj", "o_proj"]
Models selection
For comparison, 2 models were chosen: small smolLm2 with 135M parameters and middle-size model - phi2 from microsoft with 2.7B parameters.
Evaluation
For evaluation, we used comparison of model’s prediction with the actual answer. In order to use this evaluation model had to learn a dataset formatting - ‘####’ in the end after wich the numerical answer is provided.
Results
Baseline
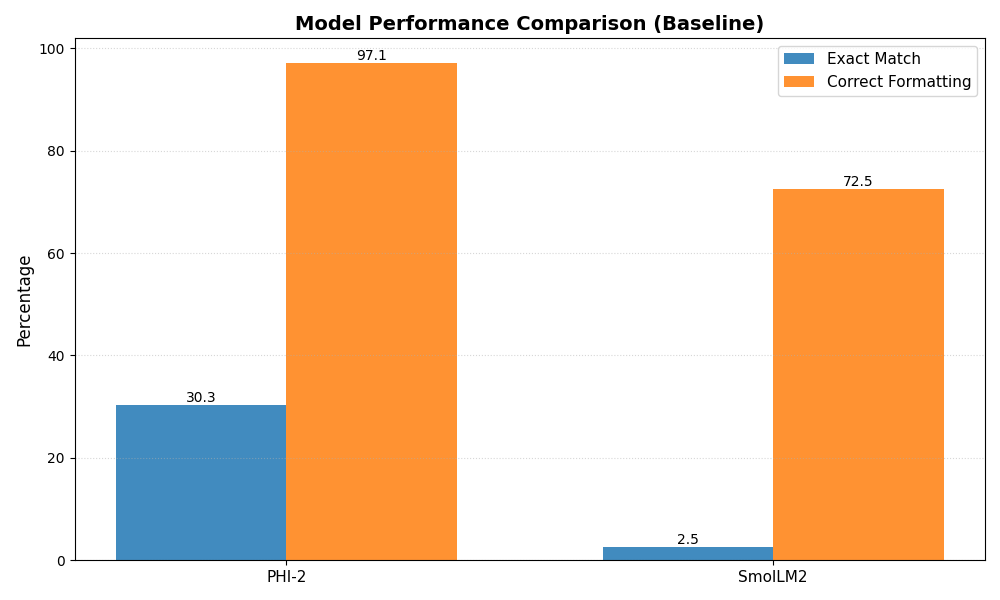
Baseline results are based on the regular fine-tuning of models on the whole dataset. PHI2 demonstrated 30.27% answer accuracy and 97.07% formatting accuracy, whereas smolLM2 2.54% answer accuracy and 72.46% formatting accuracy
Curriculum learning
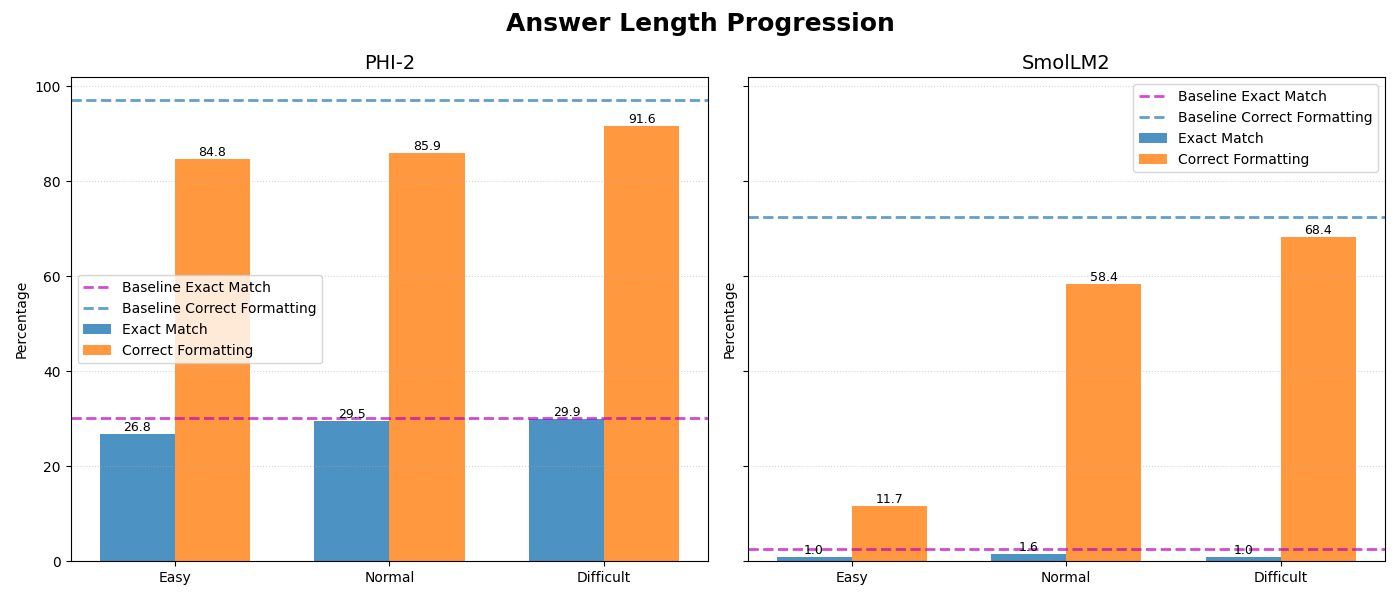
The naive (answer length-based) fine-tuning approach has shown the following results:
After ‘easy’ stage: smolLM2: 0.98 (-1.56%) - answer accuracy, 11.72 (-60.74%) - formatting accuracy; PHI2: 26.76 (-3.51%) - answer accuracy, 84.77 (-12.30%) - formatting accuracy
After ‘normal’ stage: smolLM2: 1.56 (-0.98%) - answer accuracy, 58.40 (-14.06%) - formatting accuracy PHI2: 29.49 (-0.78%) - answer accuracy, 85.94 (-11.13%) - formatting accuracy
After ‘difficult’ stage: smolLM2: 0.98 (-1.56%) - answer accuracy, 68.36 (-4.10%) - formatting accuracy PHI2: 29.88 (-0.39%) - answer accuracy, 91.6 (-5.47%) - formatting accuracy
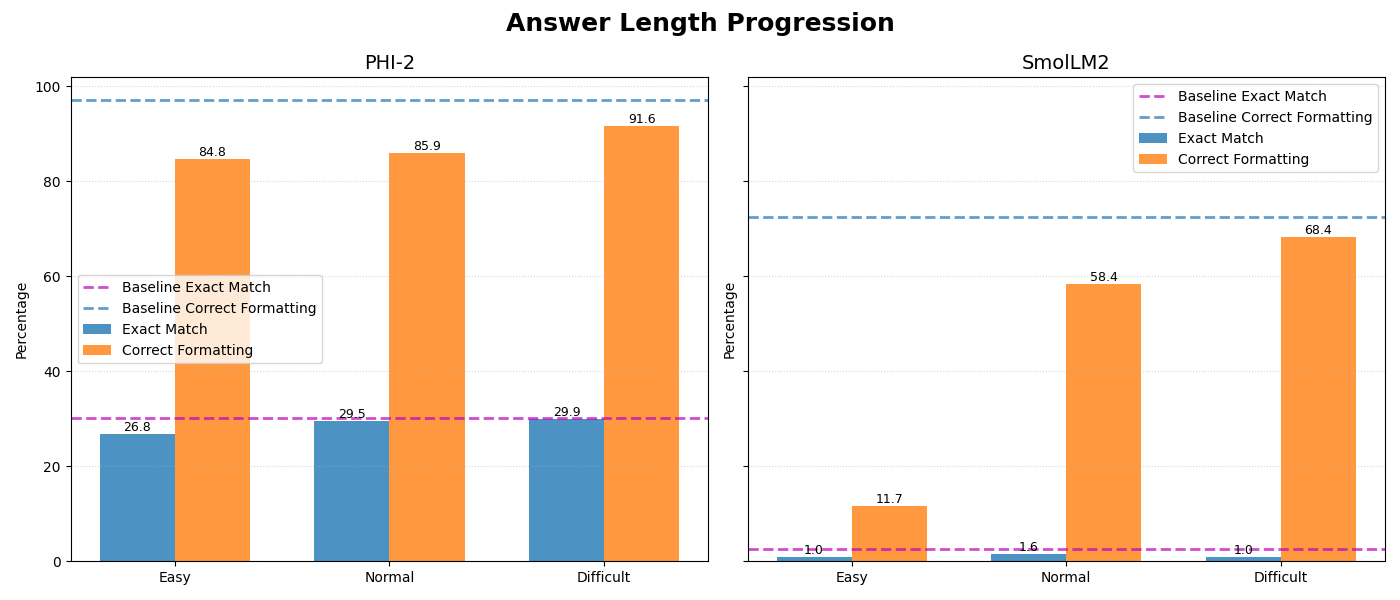
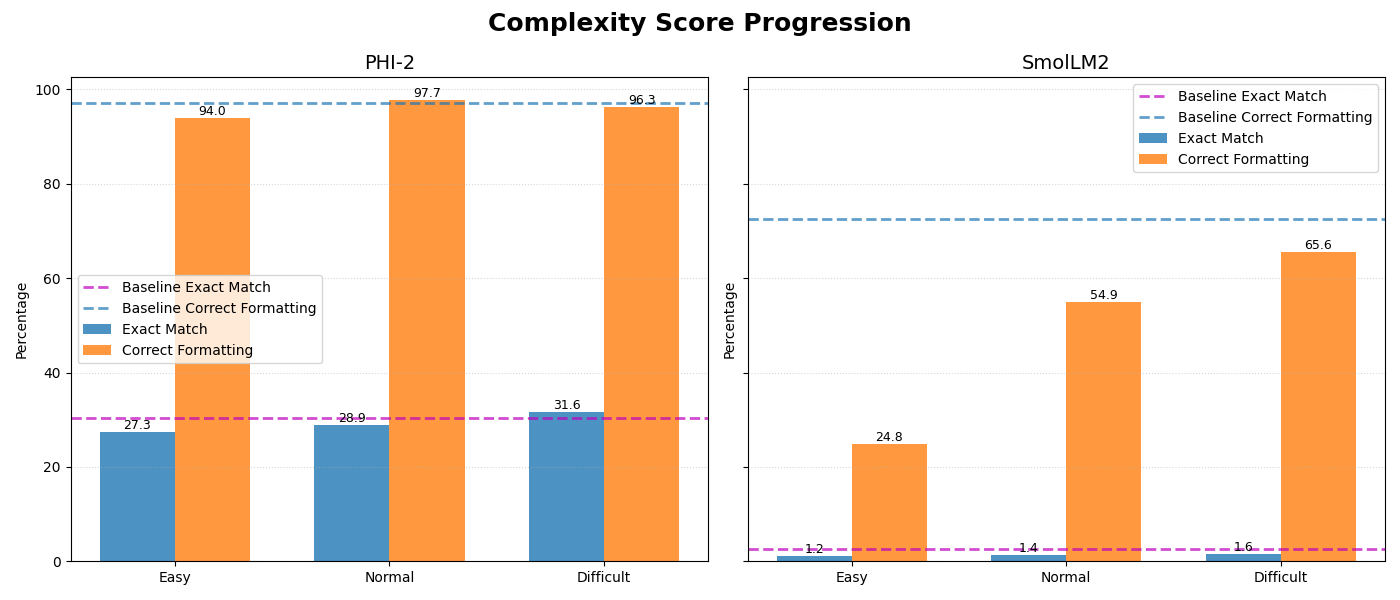
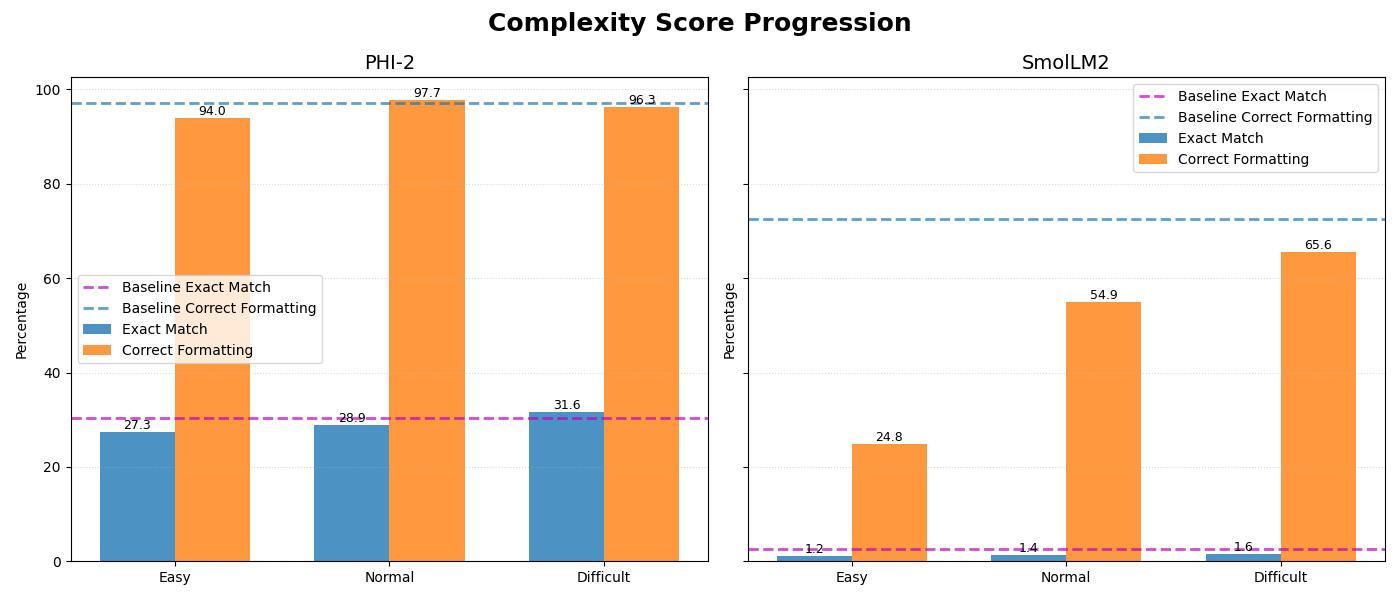
For the more advanced curriculum results are:
After ‘easy’ stage: smolLM2: 1.17 (-1.37%) - answer accuracy, 24.80 (-47.66%) - formatting accuracy; PHI2: 27.34 (-2.93%) - answer accuracy, 93.95 (-3.12%) - formatting accuracy
After ‘normal’ stage: smolLM2: 1.37 (-1.17%) - answer accuracy, 54.88 (-17.58%) - formatting accuracy; PHI2: 28.91 (-1.36%) - answer accuracy, 97.66 (+0.59%) - formatting accuracy
After ‘difficult’ stage: smolLM2: 1.56 (-0.98%) - answer accuracy, 65.63 (-6.83%) - formatting accuracy; PHI2: 31.64 (+1.37%) - answer accuracy, 96.29 (-0.78%) - formatting accuracy
Naive (Answer Length-Based) Fine-Tuning Results
| Stage | Model | Answer Accuracy | Change (%) | Formatting Accuracy | Change (%) |
|---|---|---|---|---|---|
| Easy | smolLM2 | 0.98 | -1.56% | 11.72 | -60.74% |
| PHI2 | 26.76 | -3.51% | 84.77 | -12.30% | |
| Normal | smolLM2 | 1.56 | -0.98% | 58.40 | -14.06% |
| PHI2 | 29.49 | -0.78% | 85.94 | -11.13% | |
| Difficult | smolLM2 | 0.98 | -1.56% | 68.36 | -4.10% |
| PHI2 | 29.88 | -0.39% | 91.60 | -5.47% |
Advanced Curriculum Fine-Tuning Results
| Stage | Model | Answer Accuracy | Change (%) | Formatting Accuracy | Change (%) |
|---|---|---|---|---|---|
| Easy | smolLM2 | 1.17 | -1.37% | 24.80 | -47.66% |
| PHI2 | 27.34 | -2.93% | 93.95 | -3.12% | |
| Normal | smolLM2 | 1.37 | -1.17% | 54.88 | -17.58% |
| PHI2 | 28.91 | -1.36% | 97.66 | +0.59% | |
| Difficult | smolLM2 | 1.56 | -0.98% | 65.63 | -6.83% |
| PHI2 | 31.64 | +1.37% | 96.29 | -0.78% |
Conclusion
Overall, these experiments showed that curriculum learning can help—but only when the curriculum actually reflects task difficulty. The naive answer-length approach consistently hurt both models, confirming that not all “easy-to-hard” progressions are meaningful.
The advanced, complexity-based curriculum did work: PHI-2 gained +1.37% answer accuracy in the final stage and even saw a small formatting boost at the Normal stage. In contrast, the 135M model showed no improvements anywhere, suggesting that very small models just don’t benefit from staged training and may even get confused by it.
The main takeaway: curriculum design matters a lot, and when it’s done right, medium-sized models like PHI-2 can squeeze out measurable gains that standard fine-tuning doesn’t provide.
